所述配对双样品的Wilcoxon检验一种的非参数检验，其可以被用于比较样品的两个独立数据。

 

本文介绍如何在ř中计算两个样本的秩检验。

可视化数据并在ř中计算的Wilcoxon测试

ř函数用于计算的秩检验

为了执行两个样本的Wilcoxon检验，比较两个独立样本（x＆y）的均值，R函数wilcox.test（）可以如下使用：

wilcox.test(x, y, alternative = "two.sided")

 

• x，y：数字向量
• 替代方案：替代假设允许值是“two.sided”（默认值），“更大”或“更少”之一。

 

将数据导入R.

1. 准备数据

2. 将数据保存在外部的.TXT选项卡或的的.csv文件中

3. 将您的数据导入ř如下：

1.  
   #

   If .txt tab file, use this
2.  
   my_data <-

   read.delim(file.choose())
3.  
   #

   Or, if .csv file, use this
4.  
   my_data <-

   read.csv(file.choose())

在这里，我们将使用一个示例数据集，其中包含18个人（9名女性和9名男性）的权重：

1.  
   #

   Data in two numeric vectors
2.  
   women_weight <-

   c(38.9, 61.2, 73.3, 21.8, 63.4, 64.6, 48.4, 48.8, 48.5)
3.  
   men_weight <-

   c(67.8, 60, 63.4, 76, 89.4, 73.3, 67.3, 61.3, 62.4)
4.  
   #

   Create a data frame
5.  
   my_data <- data.frame(
6.  
   group = rep(

   c("Woman", "Man"), each = 9),
7.  
   weight =

   c(women_weight, men_weight)
8.  
   )

我们想知道，如果女性体重的中位数与男性体重的中位数不同？

检查数据

print(my_data)

1.  
   group weight
2.  
   1

   Woman 38.9
3.  
   2

   Woman 61.2
4.  
   3

   Woman 73.3
5.  
   4

   Woman 21.8
6.  
   5

   Woman 63.4
7.  
   6

   Woman 64.6
8.  
   7

   Woman 48.4
9.  
   8

   Woman 48.8
10.  
    9

    Woman 48.5
11.  
    10

    Man 67.8
12.  
    11

    Man 60.0
13.  
    12

    Man 63.4
14.  
    13

    Man 76.0
15.  
    14

    Man 89.4
16.  
    15

    Man 73.3
17.  
    16

    Man 67.3
18.  
    17

    Man 61.3
19.  
    18

    Man 62.4

可以按组计算（中位数和四分位数间距（IQR））。可以使用dplyr包。

• 要安装dplyr软件包，请键入以下内容：

install.packages("dplyr")

• 按组计算摘要统计信息：

1.  
   library(dplyr)
2.  
   group_by(my_data,

   group) %>%
3.  
   summarise(
4.  
   count = n(),
5.  
   median = median(weight, na.rm =

   TRUE),
6.  
   IQR = IQR(weight, na.rm =

   TRUE)
7.  
   )

1.  
   Source: local data frame [2 x 4]
2.  
   group count median IQR
3.  
   (

   fctr) (int) (dbl) (dbl)
4.  
   1

   Man 9 67.3 10.9
5.  
   2

   Woman 9 48.8 15.0

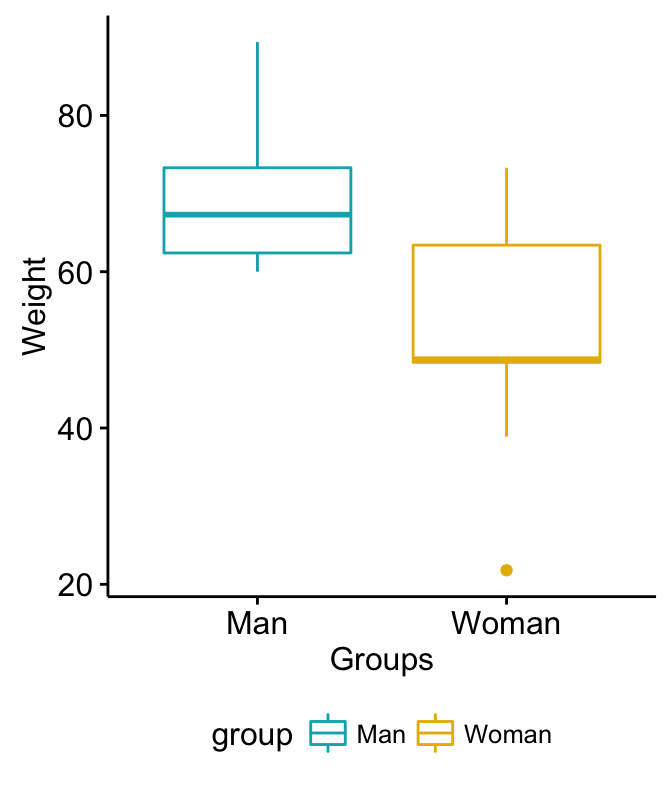
使用箱形图可视化数据

您可以按照此链接中的描述绘制R基本图：。在这里，我们将使用进行基于ggplot2的简单数据可视化

• 从GitHub上的安装最新版本的ggpubr如下（推荐）：

1.  
   # Install
2.  
   if(!require(devtools)) install.packages("devtools")
3.  
   devtools::install_github(

   "kassambara/ggpubr")

• 或者，从CRAN安装如下：

install.packages("ggpubr")

• 可视化您的数据：

1.  
   # Plot weight

   by group and color by group
2.  
   library(

   "ggpubr")
3.  
   ggboxplot(my_data, x =

   "group", y = "weight",
4.  
   color =

   "group", palette = c("#00AFBB", "#E7B800"),
5.  
   ylab =

   "Weight", xlab = "Groups")

计算不成对的双样本秩检验

问题：女性和男性体重有显着差异吗？

1）计算双样本Wilcoxon检验 - 方法1：数据保存在两个不同的数值向量中。

res <- wilcox.test(women_weight, men_weight)res

1.  
    
2.  
   Wilcoxon rank sum test

   with continuity correction
3.  
   data: women_weight

   and men_weight
4.  
   W =

   15, p-value = 0.02712
5.  
   alternative hypothesis:

   true location shift is not equal to 0

它将发出一条警告信息，称为“无法用平局计算精确的p值”。它可以通过添加另一个参数exact = FALSE来抑制此消息，但结果将是相同的。

2）计算双样本Wilcoxon检验 - 方法2：将数据保存在数据框中。

res <- wilcox.test(weight ~ group, data = my_data,                   exact = FALSE)res

1.  
    
2.  
   Wilcoxon rank sum test

   with continuity correction
3.  
   data: weight

   by group
4.  
   W =

   66, p-value = 0.02712
5.  
   alternative hypothesis:

   true location shift is not equal to 0

# Print the p-value onlyres$p.value

[1] 0.02711657

如您所见，这两种方法给出了相同的结果。

测试的p值为  0.02712，小于显着性水平α= 0.05。我们可以得出结论，男性的中位数体重与女性的中位数体重显着不同，p值  = 0.02712。

 

注意：

• 如果你想测试男性体重的中位数是否小于女性体重的中位数，请输入：

wilcox.test(weight ~ group, data = my_data,         exact = FALSE, alternative = "less")

• 或者，如果您想测试男性体重的中位数是否大于女性体重的中位数，请输入此值

wilcox.test(weight ~ group, data = my_data,        exact = FALSE, alternative = "greater")